+## 前言\r
+\r
+马拉车算法(Manacher's algorithm)是一个求一个字符串中最长回文连续子序列的算法\r
+\r
+其实是自己复习用的(\r
+\r
+## 正文\r
+\r
+[【模板】manacher算法](https://www.luogu.org/problemnew/show/P3805)\r
+\r
+题意是求S中的最长回文串\r
+\r
+最暴力的做法当然是枚举l和r,对于每个l和r求遍历一遍判断是否为回文\r
+\r
+时间复杂度达到$O(n^3)$,显然做不了这题\r
+\r
+在这个基础上稍微优化一下,也是很显然的做法:长度为奇数回文串以最中间字符的位置为对称轴左右对称,而长度为偶数的回文串的对称轴在中间两个字符之间的空隙。可以遍历这些对称轴,在每个对称轴上同时向左和向右扩展,直到左右两边的字符不同或者到达边界。\r
+\r
+这样的复杂度是$O(n^2)$,还是过不了\r
+\r
+观察数据范围,$S.length()\leq11000000$,应该需要一个$O(n)$及以下的算法\r
+\r
+dalao云\r
+>暴力算法的优化是信息的利用和对重复搜索的去重\r
+\r
+我们考虑如何利用这里的重复信息\r
+\r
+第一种解法,是直接暴力计算\r
+\r
+而第二种解法,是利用字符串对称的性质,把枚举端点变成枚举中点,少了一个循环,优化掉$O(n)$的复杂度\r
+\r
+我们所求的$O(n)$算法,是不是能由第二种解法再利用一次字符串对称的性质得来呢?\r
+\r
+观察下面的字符串:\r
+\r
+$O A K A B A K A B A O A K$\r
+\r
+其中的最长回文串为$ABAKABA$,若使用第二种解法,有什么可以不计算的呢?\r
+\r
+相信很容易猜到,一个回文串的左半边有一个回文串,那它的右半边也有一个,那么我们对这个回文串的计算显然可以略去\r
+\r
+扩展到一般性质,若一个回文串里包含着另一个回文串,那这个回文串的另一边必然存在另一个与它一模一样的回文串!\r
+\r
+由此我们来改进第二种算法\r
+\r
+这个$O(n^2)$算法有什么缺点呢?\r
+\r
+1. 回文串长度的奇偶性造成了对称轴的位置可能在某字符上,也可能在两个字符之间的空隙处,要对两种情况分别处理\r
+\r
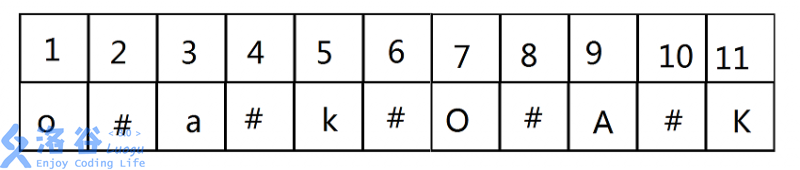
+如何解决?我们可以强行在原字符串中插入其他本字符串不会出现的字符,如"#"\r
+\r
+也就是说,若原来的字符串是这样\r
+\r
+\r
+\r
+那么我们把它改成这样\r
+\r
+\r
+\r
+关于这部分的代码:\r
+```cpp\r
+inline void change() {\r
+ s[0]=s[1]='#';\r
+ for(int i=0; i<n; i++) {\r
+ s[i*2+2]=a[i];\r
+ s[i*2+3]='#';\r
+ }\r
+ n=n*2+2;\r
+ s[n]=0;\r
+}\r
+```\r
+\r
+这样我们就可以直接以每个字符为对称轴进行扩展了\r
+\r
+2. 会出现很多子串被重复多次访问,时间效率大幅降低。\r
+\r
+这个就是我们刚刚提出的优化了。\r
+\r
+我们用一个辅助数组$hw_i$表示$i$点能够扩展出的回文长度\r
+\r
+我们先设置一个辅助变量$maxright$,表示已经触及到的最右边的字符\r
+\r
+以及一个辅助变量$mid$,表示包含$maxright$的回文串的对称轴所在的位置\r
+\r
+也就是这样:\r
+\r
+\r
+\r
+当i在maxright左边且在mid右边时:\r
+\r
+设i关于mid的对称点为j,显然$hw_i$一定不会小于$hw_j$。\r
+\r
+我们没必要保存j,j可以通过计算得出,为$mid+(mid-i)=(mid\times2)-i$\r
+\r
+那么我们就将$hw_i$设为$hw_j$,从$i+hw_i$开始扩展(利用已知信息),这样就可以较快地求出hw[i],然后重新maxright和mid\r
+\r
+当$i$在$maxright$右边时,我们无法得知关于$hw_i$的信息,只好从1开始遍历,然后更新$maxright$和$mid$\r
+\r
+这部分的代码也是非常简短的:\r
+```cpp\r
+inline void manacher() {\r
+ int maxright=0,mid;\r
+ for(int i=1; i<n; i++) {\r
+ if(i<maxright)\r
+ hw[i]=min(hw[(mid<<1)-i],hw[mid]+mid-i);\r
+ else\r
+ hw[i]=1;\r
+ while(s[i+hw[i]]==s[i-hw[i]])\r
+ ++hw[i];\r
+ if(hw[i]+i>maxright) {\r
+ maxright=hw[i]+i;\r
+ mid=i;\r
+ }\r
+ }\r
+}\r
+```\r
+虽然看起来优化不了多少,但它的时间复杂度确实是$O(n)$的\r
+\r
+## 习题\r
+[P4555 [国家集训队]最长双回文串](https://www.luogu.org/problemnew/show/P4555)\r
+\r
+一道几乎是裸题的题\r
+\r
+看到回文串可以想想马拉车,于是我们就用马拉车写\r
+\r
+在朴素的马拉车基础上求出l和r数组,$l_i$表示i所在回文串中的最右端的下标,$r_i$代表i所在回文串中的最左端的下标\r
+\r
+然后拼接一下即可:\r
+\r
+```cpp\r
+#include<iostream>\r
+#include<cstdio>\r
+#include<cstring>\r
+#include<cstring>\r
+\r
+using namespace std;\r
+\r
+const int maxn=200010;\r
+char a[maxn],s[maxn<<1];\r
+int l[maxn<<1],r[maxn<<1];\r
+int n,hw[maxn],ans;\r
+inline void manacher() {\r
+ int maxright=0,mid;\r
+ for(int i=1; i<n; ++i) {\r
+ if(i<maxright)\r
+ hw[i]=min(hw[(mid<<1)-i],hw[mid]+mid-i);\r
+ else\r
+ hw[i]=1;\r
+ while(s[i+hw[i]]==s[i-hw[i]])\r
+ ++hw[i];\r
+ if(hw[i]+i>maxright) {\r
+ maxright=hw[i]+i;\r
+ mid=i;\r
+ }\r
+ }\r
+}\r
+\r
+void change() {\r
+ s[0]=s[1]='#';\r
+ for(int i=0; i<n; ++i) {\r
+ s[i*2+2]=a[i];\r
+ s[i*2+3]='#';\r
+ }\r
+ n=n*2+2;\r
+ s[n]=0;\r
+}\r
+\r
+inline int maxx(int a,int b) {\r
+ return a>b?a:b;\r
+}\r
+\r
+int main() {\r
+ scanf("%s",a);\r
+ n=strlen(a);\r
+ change();\r
+ manacher();\r
+ int now=0;\r
+ for(int i=0; i<n; ++i)\r
+ while(now<=i+hw[i]-1)\r
+ l[now++]=i;\r
+ now=n;\r
+ for(int i=n-1; i>=0; --i) {\r
+ while(now>=i-hw[i]+1)\r
+ r[now--]=i;\r
+ }\r
+ int ans=0;\r
+ for(int i=0; i<n; ++i)\r
+ ans=maxx(ans,r[i]-l[i]);\r
+ printf("%d",ans);\r
+}\r
+```\r
 OSDN Git Service
OSDN Git Service