它每次考察数组当前部分的中间元素,如果中间元素刚好是要找的,就结束搜索过程;如果中间元素小于所查找的值,那么左侧的只会更小,不会有所查找的元素,只需要到右侧去找就好了;如果中间元素大于所查找的值,同理,右侧的只会更大而不会有所查找的元素,所以只需要到左侧去找。
-在二分搜索过程中,每次都把查询的区间减半,因此对于一个长度为 $n$ 的数组,至多会进行 $\mathcal {O}(\log n)$ 次查找。
+在二分搜索过程中,每次都把查询的区间减半,因此对于一个长度为 $n$ 的数组,至多会进行 $O(\log n)$ 次查找。
```c++
int binary_search(int start, int end, int key) {
### Dinkelbach 算法
-Dinkelbach 算法是每次用上一轮的答案当做新的 $L$ 来输入,不断地迭代,直至答案收敛。
\ No newline at end of file
+Dinkelbach 算法是每次用上一轮的答案当做新的 $L$ 来输入,不断地迭代,直至答案收敛。
### 最长回文子串
-$O(n^2)$:$dp[i] = \max(dp[j] + 1), s(j + 1 .. i)$ 是回文
+$O(n^2)$:$dp[i] = \max(dp[j] + 1), s(j + 1 \cdots i)$ 是回文
$O(n)$: Manacher
这样得到的回文串长度就保证是奇数了
-考虑如果按顺序得到了 $p[1 .. i - 1]$,如何计算 $p[i]$ 的值?
+考虑如果按顺序得到了 $p[1 \cdots i - 1]$,如何计算 $p[i]$ 的值?
-如果之前有一个位置比如说是 $id$,有 $p[id] + id > i$ 那么 $i$ 这个位置是被覆盖了的,根据 $id$ 处的对称性,我们找 $p[id * 2 - i]$ 延伸的部分被 $p[id]$ 延伸的部分所覆盖的那段,显然这段对称回去之后是可以从 $i$ 处延伸出去的长度。
+如果之前有一个位置比如说是 $id$,有 $p[id] + id > i$ 那么 $i$ 这个位置是被覆盖了的,根据 $id$ 处的对称性,我们找 $p[id \times 2 - i]$ 延伸的部分被 $p[id]$ 延伸的部分所覆盖的那段,显然这段对称回去之后是可以从 $i$ 处延伸出去的长度。
如果找不到呢?就先让 $p[i] = 1$ 吧。
#### 思路一:
-$dp[i][j] \ 表示\ 1..i\ 和\ 1..j\ 两条路径$。
+$dp[i][j]$ 表示 $1 \cdots i$ 和 $1 \cdots j$ 两条路径。
-我们可以人为要求 $1..i$ 是更快的那一条路径。
+我们可以人为要求 $1 \cdots i$ 是更快的那一条路径。
这样考虑第 $i$ 个点分给谁。
如果是分给快的那条:
-$dp[i][j] = \min(dp[i - 1][j] + dis[i - 1][i]),\ j = 1..i$
+$dp[i][j] = \min(dp[i - 1][j] + dis[i - 1][i]),\ j = 1 \cdots i$
如果是慢的,原来是慢的那条就变成了快的,所以另一条是到 $i - 1$ 那个点:
-$dp[i][j] = \min(dp[i - 1][j] + dis[j][i]),\ j = 1..i$
+$dp[i][j] = \min(dp[i - 1][j] + dis[j][i]),\ j = 1 \cdots i$
答案是 $\min(dp[n][i] + dis[n][i])$。
(从一开始编号,终点是 $n$)
#### 思路二
-把 $dp[i][j]$ 定义反过来,不是 $1..i$ 和 $1..j$。
+把 $dp[i][j]$ 定义反过来,不是 $1 \cdots i$ 和 $1 \cdots j$。
-改成是 $i..n$ 和 $j..n$,不要求哪个更快。
+改成是 $i..n$ 和 $j \cdots n$,不要求哪个更快。
这样的转移更好写:
限制:要求相邻两行中删除的像素必须位于同一列或相邻列。
-$dp[i][j] = \min(dp[i - 1][j], dp[i - 1][j - 1], dp[i - 1][j + 1]) + cost[i][j]$
+$dp[i][j] = \min(dp[i - 1][j], dp[i - 1][j - 1], dp[i - 1][j + 1]) + cost[i][j]$
边界:$dp[1][i] = cost[1][i]$。
等价于之前那个最优二叉搜索树。
-$dp[i][j] = \min(dp[i][k] + dp[k][j]) + l[j] - l[i] + 1,\ k = i + 1\ ..\ j - 1$
+$dp[i][j] = \min(dp[i][k] + dp[k][j]) + l[j] - l[i] + 1,\ k = i + 1 \cdots j - 1$
注意 $l[i]$ 表示的是第i个切分点的位置。
\r
## 1. 记忆化搜索是啥\r
\r
-好,就以 [这道题](https://www.luogu.org/problemnew/show/P1048) 为例,我不会动态规划,只会搜索,我就会直接写一个粗暴的 [DFS](/search/dfs) :\r
+好,就以 [洛谷 P1048 采药](https://www.luogu.org/problemnew/show/P1048) 为例,我不会动态规划,只会搜索,我就会直接写一个粗暴的 [DFS](/search/dfs) :\r
\r
-* 注: 为了方便食用, 本文中所有代码省略头文件 *\r
+* 注: 为了方便食用, 本文中所有代码省略头文件\r
\r
```cpp\r
int n,t;\r
\r
---\r
\r
-** 如有疑问或质疑, 请留下评论或私信我 **\r
+** 如有疑问或质疑, 请留下评论或联系我 GitHub [@interestingLSY](https://github.com/interestingLSY) **\r
\r
** questions are welcome **\r
-\r
队列,英文名是 queue,在 C++ STL 中有 [std::queue](https://en.cppreference.com/w/cpp/container/queue) 和 [std::priority_queue](https://en.cppreference.com/w/cpp/container/priority_queue)。
-下列说法正确吗?
-
-- 先进入队列的元素一定先出队列
-
-- 先进入队列的元素一定后出队列
-
+先进入队列的元素一定先出队列
栈,英文名是 stack, C++ STL 中有 [std::stack](https://en.cppreference.com/w/cpp/container/stack),不过一般都直接用数组模拟一个栈,也十分方便。
-下列说法正确吗?
-
-- 先进入栈的元素一定先出栈
-
-- 先进入栈的元素一定后出栈
\ No newline at end of file
+先进入栈的元素一定后出栈
### 实现
-我们定义一个数组 `f[k][x][y]`,表示只允许经过结点 1~k,结点 x 到结点 y 的最短路长度
+我们定义一个数组 `f[k][x][y]`,表示只允许经过结点 $1 \cdots k$,结点 $x$ 到结点 $y$ 的最短路长度
-很显然,`f[n][x][y]`就是结点 x 到结点 y 的最短路长度
+很显然,`f[n][x][y]`就是结点 $x$ 到结点 $y$ 的最短路长度
我们来考虑怎么求这个数组
-`f[0][x][y]`:边权,或者 0,或者 $+\infty$ 【`f[0][x][x]`什么时候应该是+inf?】
+`f[0][x][y]`:边权,或者 $0$,或者 $+\infty$ 【`f[0][x][x]`什么时候应该是+inf?】
`f[k][x][y] = min(f[k-1][x][y], f[k-1][x][k]+f[k-1][k][y])`
### 实现
-假设结点为S
+假设结点为 $S$
-先定义 dist(u) 为 S 到 u (当前)的最短路径长度
+先定义 $dist(u)$ 为 $S$ 到 $u$ (当前)的最短路径长度
relax(u,v): $dist(v) = min(dist(v), dist(u) + edge_len(u, v))$
三角形不等式: $dist(v) \leq dist(u) + edge_len(u, v)$
-证明:反证法,如果不满足,那么可以用 relax 操作来更新 dist(v) 的值
+证明:反证法,如果不满足,那么可以用 relax 操作来更新 $dist(v)$ 的值
Bellman-Ford 算法如下
我们考虑最短路存在的时候
-由于一次 relax 会使(被 relax 的)最短路的边数至少 +1,而最短路的边数最多为 n-1
+由于一次 relax 会使(被 relax 的)最短路的边数至少 $+1$,而最短路的边数最多为 $n-1$
-所以最多(连续)relax n-1 次……(relax 一定是环环相扣的,不然之前就能被 relax 掉)
+所以最多(连续)relax $n-1$ 次……(relax 一定是环环相扣的,不然之前就能被 relax 掉)
-所以最多循环 n-1 次
+所以最多循环 $n-1$ 次
总时间复杂度 $O(nm)$ **【对于最短路存在的图】**
}
```
-注:这里的 edge_len(u, v) 表示边的权值,如果该边不存在则为 $+\infty$,u=v 则为 0
+注:这里的 `edge_len(u, v)` 表示边的权值,如果该边不存在则为 $+\infty$,$u=v$ 则为 $0$
### 应用
给一张有向图,问是否存在负权环
-做法很简单,跑 Bellman-Ford 算法,如果有个点被 relax 成功了 n 次,那么就一定存在
+做法很简单,跑 Bellman-Ford 算法,如果有个点被 relax 成功了 $n$ 次,那么就一定存在
-如果 n-1 次之内算法结束了,就一定不存在
+如果 $n-1$ 次之内算法结束了,就一定不存在
### 另一种实现(优化)(SPFA)
主要思想是,将结点分成两个集合:已确定最短路长度的,未确定的
-一开始第一个集合里只有 S
+一开始第一个集合里只有 $S$
然后重复这些操作
直到第二个集合为空,算法结束
-时间复杂度:只用分析集合操作,n 次 delete-min,m 次 decrease-key
+时间复杂度:只用分析集合操作,$n$ 次 delete-min,$m$ 次 decrease-key
如果用暴力: $O(n^2 + m)$
本项目受 [CTF Wiki](https://ctf-wiki.github.io/ctf-wiki/) 的启发,在编写过程中参考了诸多资料,在此一并致谢。
-本项目文档内容托管在 [Github](https://github.com/24OI/OI-wiki),主要使用 [Issues](https://github.com/24OI/OI-wiki/issues) / [QQ](https://jq.qq.com/?_wv=1027&k=5EfkM6K) / [Telegram](https://t.me/OIwiki) 进行交流沟通,期待你的加入。
+本项目文档内容托管在 [GitHub](https://github.com/24OI/OI-wiki),主要使用 [Issues](https://github.com/24OI/OI-wiki/issues) / [QQ](https://jq.qq.com/?_wv=1027&k=5EfkM6K) / [Telegram](https://t.me/OIwiki) 进行交流沟通,期待你的加入。
Telegram 群组链接为 [@OIwiki](https://t.me/OIwiki) , QQ 群号码为 [`588793226`](https://jq.qq.com/?_wv=1027&k=5EfkM6K),欢迎加入。
## Catalan 数列
-以下问题属于Catalan数列:<br>
-1. 有$2n$个人排成一行进入剧场。入场费5元。其中只有$n$个人有一张5元钞票,另外$n$人只有10元钞票,剧院无其它钞票,问有多少中方法使得只要有10元的人买票,售票处就有5元的钞票找零?<br>
-2. 一位大城市的律师在她住所以北$n$个街区和以东$n$个街区处工作。每天她走$2n$个街区去上班。如果他从不穿越(但可以碰到)从家到办公室的对角线,那么有多少条可能的道路?<br>
-3. 在圆上选择$2n$个点,将这些点成对连接起来使得所得到的$n$条线段不相交的方法数?<br>
-4. 对角线不相交的情况下,将一个凸多边形区域分成三角形区域的方法数?<br>
-5. 一个栈(无穷大)的进栈序列为$1,2,3, \cdots ,n$有多少个不同的出栈序列?<br>
-6. $n$个结点可够造多少个不同的二叉树?<br>
-7. $n$个不同的数依次进栈,求不同的出栈结果的种数?<br>
-8. $n$个$+1$和$n$个$-1$构成$2n$项$a_1,a_2, \cdots ,a_{2n}$,其部分和满足$a_1+a_2+ \cdots +a_k>=0(k=1,2,3, \cdots ,2n)$对与$n$该数列为?
+以下问题属于 Catalan 数列:<br>
+1. 有 $2n$ 个人排成一行进入剧场。入场费 5 元。其中只有$n$个人有一张5元钞票,另外 $n$ 人只有 10 元钞票,剧院无其它钞票,问有多少中方法使得只要有 10 元的人买票,售票处就有 5 元的钞票找零?<br>
+2. 一位大城市的律师在她住所以北 $n$ 个街区和以东 $n$ 个街区处工作。每天她走 $2n$ 个街区去上班。如果他从不穿越(但可以碰到)从家到办公室的对角线,那么有多少条可能的道路?<br>
+3. 在圆上选择 $2n$ 个点,将这些点成对连接起来使得所得到的 $n$ 条线段不相交的方法数?<br>
+4. 对角线不相交的情况下,将一个凸多边形区域分成三角形区域的方法数?<br>
+5. 一个栈(无穷大)的进栈序列为 $1,2,3, \cdots ,n$ 有多少个不同的出栈序列?<br>
+6. $n$ 个结点可够造多少个不同的二叉树?<br>
+7. $n$ 个不同的数依次进栈,求不同的出栈结果的种数?<br>
+8. $n$ 个 $+1$ 和 $n$ 个 $-1$ 构成 $2n$ 项 $a_1,a_2, \cdots ,a_{2n}$,其部分和满足 $a_1+a_2+ \cdots +a_k>=0(k=1,2,3, \cdots ,2n)$ 对与 $n$ 该数列为?
其对应的序列为:
该递推关系的解为:
-$$H_n=\frac{C_{2n}^{n}}{n+1}(n=1,2,3,...)$$
-
+$$H_n=\frac{C_{2n}^{n}}{n+1}(n=1,2,3,\cdots)$$
\r
### 逆序对问题\r
\r
-贡献定义为 $j=1...i-1$ 中求出 $a[j]>a[i]$。这样子朴素的算法就很简单, 只需要对 $1...i-1$ 进行遍历, 时间复杂度 $O(n^2)$。不过也有 $O(n\ log\ n)$ 的方法, 这里做下铺垫, 先讲解权值线段树的做法。\r
+贡献定义为 $j=1 \cdots i-1$ 中求出 $a[j]>a[i]$。这样子朴素的算法就很简单, 只需要对 $1 \cdots i-1$ 进行遍历, 时间复杂度 $O(n^2)$。不过也有 $O(n\ log\ n)$ 的方法, 这里做下铺垫, 先讲解权值线段树的做法。\r
\r
每加入一个数字, 我们可以把这个数字插入到权值线段树中, 如下:\r
\r
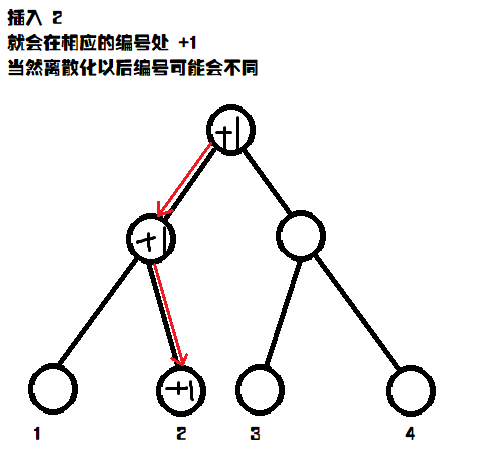\r
\r
-当到第 $i$ 个数字的时候, 我们就可以直接在权值线段树中查询 $num[i]...max$ (其中 $max$ 为 $1...i-1$ 最大的值)。这就是第 $i$ 个数的贡献。查询完以后记得要继续插入此数。\r
+当到第 $i$ 个数字的时候, 我们就可以直接在权值线段树中查询 $num[i] \cdots max$ (其中 $max$ 为 $1 \cdots i-1$ 最大的值)。这就是第 $i$ 个数的贡献。查询完以后记得要继续插入此数。\r
\r
### 权值线段树转化为树状数组\r
\r
\r
### 偏序问题的定义\r
\r
-什么是偏序? $N$ 维偏序, 也就是给你 $N$ 个数组,$i$ 的贡献定义为数组 $1$ 数组 $2.....$ 数组 $N$ 的第 $i$ 个数在这 $N$ 个数组中满足 数组 $1[i]$\r
- $2[i] .... N[i] \leq 1[j],2[j]....N[j]$。($1\leq i,j\leq N$)\r
+什么是偏序? $N$ 维偏序, 也就是给你 $N$ 个数组,$i$ 的贡献定义为数组 $1$ 数组 $2 \cdots$ 数组 $N$ 的第 $i$ 个数在这 $N$ 个数组中满足 数组 $1[i]$\r
+ $2[i] \cdots N[i] \leq 1[j],2[j] \cdots N[j]$。($1\leq i,j\leq N$)\r
\r
或许有点模糊, 我们用二维偏序来说。给定数组 $a,b$。如果 $a[j]\leq a[i]$ 且 $b[j]\leq b[i]$ 的话, 就算是一个贡献。$N$ 维也是如此。\r
\r
\r
$CDQ$ 大体可以认为是 先算出 $l \cdots mid$ 的贡献, 然后算出 $l$ 对 $r$ 的贡献, 最后再算 $mid \cdots r$ 的贡献。对于 $l \cdots mid$ 和 $mid \cdots r$ 的贡献, 可以直接 $CDQ(l,mid),CDQ(r,mid)$。为什么呢? 因为分治以后它们会对自己的 $l \cdots r$ 算自己的贡献, 所以这样子木有问题。现在讨论的重点就是如何求出 $l \cdots r$ 的贡献。\r
\r
-三维偏序问题: 偏序问题的第一维, 我们是直接排序的。注意要按第 $1$ 个数组为第 $1$ 关键字, 第 $2$ 个为第 $2$ 个关键字 $.....$。然后我们就可以保证整个数组 $a[i]\leq a[j]\ (i\leq j)$。我们现在有一个区间 $l,r$ , 我们先 $CDQ(l,mid)$。随后我们给 $l,r$ 这个区间进行编号, $num[i]:=i$(这个时候 $num$ 为编号)。我们再用一个数组 $element[l \cdots r]$ 为 $l \cdots r$ 的 $b[i]$, 然后进行 $Sort(l,r)$。其中 $element$ 为第一关键字, $num$ 为第二关键字。\r
+三维偏序问题: 偏序问题的第一维, 我们是直接排序的。注意要按第 $1$ 个数组为第 $1$ 关键字, 第 $2$ 个为第 $2$ 个关键字...... 然后我们就可以保证整个数组 $a[i]\leq a[j]\ (i\leq j)$。我们现在有一个区间 $l,r$ , 我们先 $CDQ(l,mid)$。随后我们给 $l,r$ 这个区间进行编号, $num[i]:=i$(这个时候 $num$ 为编号)。我们再用一个数组 $element[l \cdots r]$ 为 $l \cdots r$ 的 $b[i]$, 然后进行 $Sort(l,r)$。其中 $element$ 为第一关键字, $num$ 为第二关键字。\r
\r
-最后循环扫一遍, 因为这个时候后已经满足 $b[i]\leq b[j]\ (i\leq j)$。我们就可以按照逆序对这样子, 对权值线段树 (树状数组) 插入第三维 $c[i]$。如果 $num[i]\leq mid$ 的话, 我们就插入, 否则算贡献。为什么这样子呢? 因为现在满足的是 $b[i]\leq b[j]\ (i\leq j)$ , 而 $num[i]\leq mid$ 可以满足 $a[l .. mid]\leq a[mid+1 .. r]$, 我们只需要对 $c$ 数组进行逆序对一样的操作。\r
+最后循环扫一遍, 因为这个时候后已经满足 $b[i]\leq b[j]\ (i\leq j)$。我们就可以按照逆序对这样子, 对权值线段树 (树状数组) 插入第三维 $c[i]$。如果 $num[i]\leq mid$ 的话, 我们就插入, 否则算贡献。为什么这样子呢? 因为现在满足的是 $b[i]\leq b[j]\ (i\leq j)$ , 而 $num[i]\leq mid$ 可以满足 $a[l \cdots mid]\leq a[mid+1 \cdots r]$, 我们只需要对 $c$ 数组进行逆序对一样的操作。\r
\r
```cpp\r
void CDQ(int l,int r) {\r
}\r
```\r
\r
-$a[l..mid]\leq a[mid+1..r]$ 是只能算出 $l$ 对 $r$ 的贡献的, 所以就需要分治啦。最后别忘了还原树状数组和 $CDQ(mid+1,r)$!!! 加上树状数组时间复杂度 $O(n\ (log\ n)^2)$。\r
+$a[l \cdots mid]\leq a[mid+1 \cdots r]$ 是只能算出 $l$ 对 $r$ 的贡献的, 所以就需要分治啦。最后别忘了还原树状数组和 $CDQ(mid+1,r)$!!! 加上树状数组时间复杂度 $O(n\ (log\ n)^2)$。\r
\r
三维偏序就如此, 谢谢大家。\r
-在默认情况下,cin(cout)是极为迟缓的读入(输出)方式,而scanf(printf)比cin(cout)快得多。
+在默认情况下,`cin(cout)` 是极为迟缓的读入(输出)方式,而 `scanf(printf)` 比 `cin(cout)` 快得多。
可是为什么会这样呢?有没有什么办法解决读入输出缓慢的问题呢?
### sync_with_stdio
-这个函数是一个“是否兼容stdio”的开关,C++为了兼容C,保证程序在使用了std::printf和std::cout的时候不发生混乱,将输出流绑到了一起。
+这个函数是一个“是否兼容 stdio”的开关,C++ 为了兼容 C,保证程序在使用了 `std::printf` 和 `std::cout` 的时候不发生混乱,将输出流绑到了一起。
-这其实是C++为了兼容而采取的保守措施。我们可以在IO之前将stdio解除绑定,这样做了之后要注意不要同时混用cout和printf之类
+这其实是 C++ 为了兼容而采取的保守措施。我们可以在 IO 之前将 stdio 解除绑定,这样做了之后要注意不要同时混用 `cout` 和 `printf` 之类
### tie
-tie是将两个stream绑定的函数,空参数的话返回当前的输出流指针。
+tie 是将两个 stream 绑定的函数,空参数的话返回当前的输出流指针。
-在默认的情况下cin绑定的是cout,每次执行 << 操作符的时候都要调用flush,这样会增加IO负担。可以通过tie(0)(0表示NULL)来解除cin与cout的绑定,进一步加快执行效率。
+在默认的情况下 `cin` 绑定的是 `cout`,每次执行 `<<` 操作符的时候都要调用 `flush`,这样会增加 IO 负担。可以通过`tie(0)`(0表示 NULL)来解除 `cin` 与 `cout` 的绑定,进一步加快执行效率。
### 代码实现
## 读入优化
-scanf和printf依然有优化的空间,这就是本章所介绍的内容——读入和输出优化。
+`scanf` 和 `printf` 依然有优化的空间,这就是本章所介绍的内容——读入和输出优化。
* 注意,读入和输出优化均针对整数,不支持其他类型的数据
### 原理
-众所周知,getchar()是用来读入char类型,且速度很快,用“读入字符——转换为整形”来代替缓慢的读入
+众所周知,`getchar` 是用来读入 char 类型,且速度很快,用“读入字符——转换为整形”来代替缓慢的读入
每个整数由两部分组成——符号和数字
-整数的’+’通常是省略的,且不会对后面数字所代表的值产生影响,而’-’不可省略,因此要进行判定
+整数的 '+' 通常是省略的,且不会对后面数字所代表的值产生影响,而 '-' 不可省略,因此要进行判定
-10进制整数中是不含空格或除0~9和正负号外的其他字符的,因此在读入不应存在于整数中的字符(通常为空格)时,就可以判定已经读入结束
+10 进制整数中是不含空格或除 0~9 和正负号外的其他字符的,因此在读入不应存在于整数中的字符(通常为空格)时,就可以判定已经读入结束
### 代码实现
* 举例
-读入num 可写为 num=read();
+读入 num 可写为 `num=read();`
## 输出优化
### 原理
-同样是众所周知,putchar()是输出单个字符,其速度远快于其它输出方式
+同样是众所周知,`putchar` 是输出单个字符,其速度远快于其它输出方式
因此将数字的每一位转化为字符输出以加速
* 举例
-输出num可写为write(num);
+输出 num 可写为 `write(num);`
也可以写成非递归的形式,来得到更好的效果。
## 更快的读入/输出优化
-通过`fread`或者`mmap`可以实现更快的读入和输出。其本质为一次性读入/输出一个巨大的缓存区,如此比一个一个字符读入输出要快的多(`getchar`,`putchar`)。
+通过 `fread` 或者 `mmap` 可以实现更快的读入和输出。其本质为一次性读入/输出一个巨大的缓存区,如此比一个一个字符读入输出要快的多(`getchar`,`putchar`)。
-更通用的是`fread`,因为`mmap`不能在Windows使用。
+更通用的是 `fread`,因为 `mmap` 不能在 Windows 使用。
`fread`类似于`scanf("%s")`,不过它更为快速,而且可以一次性读入若干个字符(包括空格换行等制表符),如果缓存区足够大,甚至可以一次性读入整个文件。
std::size_t fwrite( const void* buffer, std::size_t size, std::size_t count, std::FILE* stream );
```
-使用示例:`fread(Buf, 1, MAXSIZE, stdin)`,如此从stdin文件流中读入MAXSIZE个字符到Buf中。
+使用示例:`fread(Buf, 1, MAXSIZE, stdin)`,如此从 stdin 文件流中读入 MAXSIZE 个字符到 Buf 中。
-读入之后的使用就跟普通的读入优化相似了,只需要重定义一下getchar。它原来是从文件中读入一个char,现在变成从Buf中读入一个char,也就是头指针向后移动一位。
+读入之后的使用就跟普通的读入优化相似了,只需要重定义一下 getchar。它原来是从文件中读入一个 char,现在变成从 Buf中读入一个 char,也就是头指针向后移动一位。
```cpp
char Buf[MASIZE], *S = Buf;
}
```
-`fwrite`也是类似的,先放入一个`OutBuf[MAXSIZE]` 中,最后通过`fwrite`一次性将`OutBuf`输出。
+`fwrite` 也是类似的,先放入一个 `OutBuf[MAXSIZE]` 中,最后通过 `fwrite` 一次性将 `OutBuf` 输出。
-注意`fread`必须使用文件读入,但是`fwrite`不需要。
+注意 `fread` 必须使用文件读入,但是 `fwrite` 不需要。
参考代码:
```
-Kirchhoff矩阵树定理(简称矩阵树定理)解决了一张图的生成树个数计数问题。
+Kirchhoff 矩阵树定理(简称矩阵树定理)解决了一张图的生成树个数计数问题。
## 本篇记号声明
### 无向图情况
-设$G$是一个有$n$个顶点的无向图。定义度数矩阵$D(G)$为:
+设 $G$ 是一个有 $n$ 个顶点的无向图。定义度数矩阵 $D(G)$ 为:
$$D_{ii}(G) = \mathrm{deg}(i), D_{ij} = 0, i\neq j$$
-设$\#e(i,j)$为点$i$与点$j$相连的边数,并定义邻接矩阵$A$为:
+设 $\#e(i,j)$ 为点 $i$ 与点 $j$ 相连的边数,并定义邻接矩阵 $A$ 为:
$$A_{ij}(G)=\#e(i,j), i\neq j$$
-定义Laplace矩阵(亦称Kirchhoff矩阵)$L$为:
+定义 Laplace 矩阵(亦称 Kirchhoff 矩阵)$L$为:
$$L(G) = D(G) - A(G)$$
-记图$G$的所有生成树个数为$t(G)$。
+记图 $G$ 的所有生成树个数为 $t(G)$。
### 有向图情况
-设$G$是一个有$n$个顶点的有向图。定义出度矩阵$D^{out}(G)$为:
+设 $G$ 是一个有 $n$ 个顶点的有向图。定义出度矩阵 $D^{out}(G)$ 为:
$$D^{out}_{ii}(G) = \mathrm{deg^{out}}(i), D^{out}_{ij} = 0, i\neq j$$
-类似地定理入度矩阵$D^{in}(G)$
+类似地定理入度矩阵 $D^{in}(G)$
-设$\#e(i,j)$为点$i$指向点$j$的有向边数,并定义邻接矩阵$A$为:
+设 $\#e(i,j)$ 为点 $i$ 指向点 $j$ 的有向边数,并定义邻接矩阵 $A$ 为:
$$A_{ij}(G)=\#e(i,j), i\neq j$$
-定义出度Laplace矩阵$L^{out}$为:
+定义出度 Laplace 矩阵 $L^{out}$ 为:
$$L^{out}(G) = D^{out}(G) - A(G)$$
-类似地定义入度Laplace矩阵$L^{in}$。
+类似地定义入度 Laplace 矩阵 $L^{in}$。
-记图$G$的以$r$为根的所有根向树形图个数为$t^{root}(G,r)$。所谓根向树形图,是说这张图的基图是一棵树,所有的边全部指向父亲。
+记图 $G$ 的以 $r$ 为根的所有根向树形图个数为 $t^{root}(G,r)$。所谓根向树形图,是说这张图的基图是一棵树,所有的边全部指向父亲。
-记图$G$的以$r$为根的所有叶向树形图个数为$t^{leaf}(G,r)$。所谓叶向树形图,是说这张图的基图是一棵树,所有的边全部指向儿子。
+记图 $G$ 的以 $r$ 为根的所有叶向树形图个数为 $t^{leaf}(G,r)$。所谓叶向树形图,是说这张图的基图是一棵树,所有的边全部指向儿子。
## 定理叙述
-矩阵树定理具有多种形式。其中用得较多的是定理1、定理3与定理4。
+矩阵树定理具有多种形式。其中用得较多的是定理 1、定理 3 与定理 4。
-**定理1 (矩阵树定理,无向图行列式形式)** 对于任意的$i$,都有
+**定理 1 (矩阵树定理,无向图行列式形式)** 对于任意的 $i$,都有
-$$t(G) = \det L(G)\binom{1,2,...,i-1,i+1,...,n}{1,2,...,i-1,i+1,...,n}$$
+$$t(G) = \det L(G)\binom{1,2,\cdots,i-1,i+1,\cdots,n}{1,2,\cdots,i-1,i+1,\cdots,n}$$
-其中记号$L(G)\binom{1,2,...,i-1,i+1,...,n}{1,2,...,i-1,i+1,...,n}$表示矩阵$L(G)$的第$1,...,i-1,i+1,...,n$行与第$1,...,i-1,i+1,...,n$列构成的子矩阵。也就是说,无向图的Laplace矩阵具有这样的性质,它的所有$n-1$阶主子式都相等。
+其中记号 $L(G)\binom{1,2,\cdots,i-1,i+1,\cdots,n}{1,2,\cdots,i-1,i+1,\cdots,n}$ 表示矩阵 $L(G)$ 的第 $1,\cdots,i-1,i+1,\cdots,n$ 行与第 $1,\cdots,i-1,i+1,\cdots,n$ 列构成的子矩阵。也就是说,无向图的 Laplace 矩阵具有这样的性质,它的所有 $n-1$ 阶主子式都相等。
-**定理2 (矩阵树定理,无向图特征值形式)** 设$\lambda_1, \lambda_2, ..., \lambda_{n-1}$为$L(G)$的$n - 1$个非零特征值,那么有
+**定理 2 (矩阵树定理,无向图特征值形式)** 设 $\lambda_1, \lambda_2, \cdots, \lambda_{n-1}$ 为 $L(G)$ 的 $n - 1$ 个非零特征值,那么有
-$$t(G) = \frac{1}{n}\lambda_1\lambda_2...\lambda_{n-1}$$
+$$t(G) = \frac{1}{n}\lambda_1\lambda_2\cdots\lambda_{n-1}$$
-**定理3 (矩阵树定理,有向图根向形式)** 对于任意的$k$,都有
+**定理 3 (矩阵树定理,有向图根向形式)** 对于任意的 $k$,都有
-$$t^{root}(G,k) = \det L^{out}(G)\binom{1,2,...,k-1,k+1,...,n}{1,2,...,k-1,k+1,...,n}$$
+$$t^{root}(G,k) = \det L^{out}(G)\binom{1,2,\cdots,k-1,k+1,\cdots,n}{1,2,\cdots,k-1,k+1,\cdots,n}$$
-因此如果要统计一张图所有的根向树形图,只要枚举所有的根$k$并对$t^{root}(G,k)$求和即可。
+因此如果要统计一张图所有的根向树形图,只要枚举所有的根 $k$ 并对 $t^{root}(G,k)$ 求和即可。
-**定理4 (矩阵树定理,有向图叶向形式)** 对于任意的$k$,都有
+**定理 4 (矩阵树定理,有向图叶向形式)** 对于任意的 $k$,都有
-$$t^{leaf}(G,k) = \det L^{in}(G)\binom{1,2,...,k-1,k+1,...,n}{1,2,...,k-1,k+1,...,n}$$
+$$t^{leaf}(G,k) = \det L^{in}(G)\binom{1,2,\cdots,k-1,k+1,\cdots,n}{1,2,\cdots,k-1,k+1,\cdots,n}$$
-因此如果要统计一张图所有的叶向树形图,只要枚举所有的根$k$并对$t^{leaf}(G,k)$求和即可。
+因此如果要统计一张图所有的叶向树形图,只要枚举所有的根 $k$ 并对 $t^{leaf}(G,k)$ 求和即可。
## 定理的应用
### 直接利用本定理
-!!! 例题1
- [HEOI2015]小Z的房间,请参考https://www.lydsy.com/JudgeOnline/problem.php?id=4031
+!!! 例题 1
+ [HEOI2015]小 Z 的房间,请参考https://www.lydsy.com/JudgeOnline/problem.php?id=4031
-**解** 矩阵树定理的裸题。将每个空房间看作一个结点,根据输入的信息建图,得到Laplace矩阵后,任意删掉L的第$i$行第$i$列,求这个子式的行列式即可。求行列式的方法就是高斯消元成上三角阵然后算对角线积。另外本题需要在模$k$的整数子环$\mathbb{Z}_k$上进行高斯消元,采用辗转相除法即可。
+**解** 矩阵树定理的裸题。将每个空房间看作一个结点,根据输入的信息建图,得到Laplace矩阵后,任意删掉L的第 $i$ 行第 $i$ 列,求这个子式的行列式即可。求行列式的方法就是高斯消元成上三角阵然后算对角线积。另外本题需要在模 $k$ 的整数子环 $\mathbb{Z}_k$ 上进行高斯消元,采用辗转相除法即可。
-!!! 例题2
+!!! 例题 2
[FJOI2007]轮状病毒。请参考https://www.lydsy.com/JudgeOnline/problem.php?id=1002
-**解** 本题的解法很多,这里用矩阵树定理是最直接的解法。当输入为$n$时,容易写出其$n+1$阶的Laplace矩阵为:
+**解** 本题的解法很多,这里用矩阵树定理是最直接的解法。当输入为 $n$ 时,容易写出其 $n+1$ 阶的Laplace矩阵为:
$$
L_n = \begin{bmatrix}
\end{bmatrix}_{n+1}
$$
-求出它的$n$阶子式的行列式即可,剩下的只有高精度计算了。
+求出它的 $n$ 阶子式的行列式即可,剩下的只有高精度计算了。
-!!! 例题2'
- 将例题2的数据加强,要求$n\leq 100000$,但是答案对1000007取模。(本题求解需要一些线性代数知识)
+!!! 例题 2'
+ 将例题 2 的数据加强,要求 $n\leq 100000$,但是答案对 1000007 取模。(本题求解需要一些线性代数知识)
-**解** 注意到$L_n$删掉第1行第1列以后得到的矩阵很有规律,因此其实就是在求矩阵
+**解** 注意到 $L_n$ 删掉第 1 行第 1 列以后得到的矩阵很有规律,因此其实就是在求矩阵
$$
M_n = \begin{bmatrix}
\end{bmatrix}_{n}
$$
-的行列式。对$M_n$的行列式按第一列展开,得到
+的行列式。对 $M_n$ 的行列式按第一列展开,得到
$$
\det M_n = 3\det \begin{bmatrix}
\end{bmatrix}_{n-1}
$$
-上述三个矩阵的行列式记为$d_{n-1}, a_{n-1}, b_{n-1}$。注意到$d_n$是三对角行列式,采用类似的展开的方法可以得到$d_n$具有递推公式$d_n=3d_{n-1}-d_{n-2}$。类似地,采用展开的方法可以得到$a_{n-1}=-d_{n-2}-1$,以及$(-1)^n b_{n-1}=-d_{n-2}-1$。将这些递推公式代入上式,得到
+上述三个矩阵的行列式记为 $d_{n-1}, a_{n-1}, b_{n-1}$。注意到 $d_n$ 是三对角行列式,采用类似的展开的方法可以得到 $d_n$ 具有递推公式 $d_n=3d_{n-1}-d_{n-2}$。类似地,采用展开的方法可以得到 $a_{n-1}=-d_{n-2}-1$,以及 $(-1)^n b_{n-1}=-d_{n-2}-1$。将这些递推公式代入上式,得到
$$\det M_n = 3d_{n-1}-2d_{n-2}-2$$
$$d_n = 3d_{n-1}-d_{n-2}$$
-于是猜测$\det M_n$也是非齐次的二阶线性递推。采用待定系数法可以得到最终的递推公式为
+于是猜测 $\det M_n$ 也是非齐次的二阶线性递推。采用待定系数法可以得到最终的递推公式为
$$\det M_n = 3\det M_{n-1} - \det M_{n-2} + 2$$
-改写成$(\det M_n+2) = 3(\det M_{n-1}+2) - (\det M_{n-2} + 2)$后,采用矩阵快速幂即可求出答案。
+改写成 $(\det M_n+2) = 3(\det M_{n-1}+2) - (\det M_{n-2} + 2)$ 后,采用矩阵快速幂即可求出答案。
### 与其它问题相结合
## 注释
-根向树形图在一些地方被称为内向树形图,但因为计算内向树形图用的是出度,为了不引起in和out的混淆,所以采用了根向这一说法。
+根向树形图在一些地方被称为内向树形图,但因为计算内向树形图用的是出度,为了不引起 in 和 out 的混淆,所以采用了根向这一说法。
\r
接着就到了莫队算法的精髓了,下面我们用通俗易懂的初中方法来证明它的时间复杂度是 $O(n\sqrt{n})$;\r
\r
-证:令每一块中 $L$ 的最大值为 $max_1,max_2,max_3,..., max_{\operatorname{ceil}(\sqrt{n})}$。\r
+证:令每一块中 $L$ 的最大值为 $max_1,max_2,max_3, \cdots , max_{\operatorname{ceil}(\sqrt{n})}$。\r
\r
-由第一次排序可知,$max_1 \le max_2 \le ... \le max_{\operatorname{ceil}(\sqrt{n})}$。\r
+由第一次排序可知,$max_1 \le max_2 \le \cdots \le max_{\operatorname{ceil}(\sqrt{n})}$。\r
\r
显然,对于每一块暴力求出第一个询问的时间复杂度为 $O(n)$。\r
\r
\r
$$\r
\begin{aligned}\r
-对于 L 的总时间复杂度为 & = O(\sqrt{n}(max_1-1)+\sqrt{n}(max_2-max_1)+\sqrt{n}(max_3-max_2)+...+\sqrt{n}(max_{\operatorname{ceil}(\sqrt{n})}-max_{\operatorname{ceil}(\sqrt{n})-1))} \\\\\r
-& = O(\sqrt{n}*(max_1-1+max_2-max_1+max_3-max_2+...+max_{\operatorname{ceil}(\sqrt{n})-1}-max_{\operatorname{ceil}(\sqrt{n})-2}+max_{\operatorname{ceil}(\sqrt{n})}-max_{\operatorname{ceil}(\sqrt{n})-1)}) \\\\\r
+对于 L 的总时间复杂度为 & = O(\sqrt{n}(max_1-1)+\sqrt{n}(max_2-max_1)+\sqrt{n}(max_3-max_2)+\cdots+\sqrt{n}(max_{\operatorname{ceil}(\sqrt{n})}-max_{\operatorname{ceil}(\sqrt{n})-1))} \\\\\r
+& = O(\sqrt{n}*(max_1-1+max_2-max_1+max_3-max_2+\cdots+max_{\operatorname{ceil}(\sqrt{n})-1}-max_{\operatorname{ceil}(\sqrt{n})-2}+max_{\operatorname{ceil}(\sqrt{n})}-max_{\operatorname{ceil}(\sqrt{n})-1)}) \\\\\r
& = O(\sqrt{n}*(max_{\operatorname{ceil}(\sqrt{n})-1}))\r
\end{aligned}\r
$$\r
当 $M >> n$ 时,总错误率接近于$\frac{n}{M}$
-当 $M = n$ 时,接近于 $1-1/e (≈0.63)$
+当 $M = n$ 时,接近于 $1-\frac{1}{e} (≈0.63)$
如果不是独立的,最坏情况也就是全部加起来,等于 $\frac{n}{M}$
要改进错误率,可以增加 $M$
-选取一个大的M,或者两个互质的小的 $M$
+选取一个大的 $M$,或者两个互质的小的 $M$
时间复杂度不变,单次错误率平方
对于模式串 $b$,定义 $next[]$
-$$next[i] = \max\{j\}\ s.t.\ 0 \leq j<i\ \&\&\ b[0..j-1]=b[i-j..i-1]$$
+$$next[i] = \max\{j\}\ s.t.\ 0 \leq j<i\ \&\&\ b[0 \cdots j-1]=b[i-j \cdots i-1]$$
【注意下标从 $0$ 开始】【需要画图】
基础:显然 $next[1]=0$
-归纳:如果已知 $next[0..i-1]$,那么 $next[i]=next[i-1]+1$ 或 $next[next[i-1]]+1$ 或…
+归纳:如果已知 $next[0 \cdots i-1]$,那么 $next[i]=next[i-1]+1$ 或 $next[next[i-1]]+1$ 或…
这算法的复杂度是多少?
 OSDN Git Service
OSDN Git Service